指数函数基本公式大全,全面解析与深度解读

你有没有想过，数学的世界里，有一种函数，它的增长速度比兔子繁殖还快，比病毒传播还迅猛？没错，就是指数函数！今天，就让我带你走进指数函数的奇妙世界，一起探索它的基本公式大全吧！

指数函数的起源

指数函数的历史悠久，最早可以追溯到古希腊时期。不过，真正让指数函数成为数学界明星的是17世纪的法国数学家皮埃尔·德·费马和布莱士·帕斯卡。他们发现了指数函数在解决某些数学问题时的强大能力。从此，指数函数开始在数学、物理、工程、经济学等领域大放异彩。

指数函数的定义

指数函数是一种特殊的函数，它的形式为：\\( f(x) = a^x \\)，其中 \\( a \\) 是一个正实数，且 \\( a \

eq 1 \\)，\\( x \\) 是实数。简单来说，指数函数就是将底数 \\( a \\) 乘以自身 \\( x \\) 次的结果。

指数函数的基本公式

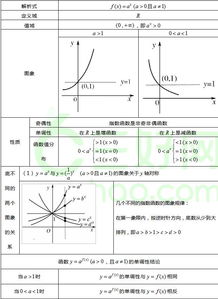
指数函数的基本公式有很多，下面就来一一揭晓它们的神秘面纱。

1. 指数函数的幂运算公式

\\( (a^m)^n = a^{mn} \\)

这个公式告诉我们，指数函数的幂运算可以简化。比如，\\( (2^3)^2 \\) 就等于 \\( 2^{3 \\times 2} \\)，也就是 \\( 2^6 \\)。

2. 指数函数的乘法公式

\\( a^m \\times a^n = a^{m n} \\)

这个公式揭示了指数函数乘法的奥秘。比如，\\( 2^3 \\times 2^4 \\) 就等于 \\( 2^{3 4} \\)，也就是 \\( 2^7 \\)。

3. 指数函数的除法公式

\\( \\frac{a^m}{a^n} = a^{m-n} \\)

这个公式告诉我们，指数函数的除法也可以简化。比如，\\( \\frac{2^5}{2^2} \\) 就等于 \\( 2^{5-2} \\)，也就是 \\( 2^3 \\)。

4. 指数函数的倒数公式

\\( a^{-m} = \\frac{1}{a^m} \\)

这个公式揭示了指数函数倒数的秘密。比如，\\( 2^{-3} \\) 就等于 \\( \\frac{1}{2^3} \\)，也就是 \\( \\frac{1}{8} \\)。

5. 指数函数的对数公式

\\( a^x = b \\) 的解为 \\( x = \\log_a b \\)

这个公式是指数函数与对数函数之间的重要联系。它告诉我们，指数函数的解可以通过对数函数来求解。比如，\\( 2^x = 8 \\) 的解就是 \\( x = \\log_2 8 \\)，也就是 \\( x = 3 \\)。

指数函数的应用

指数函数在现实生活中的应用非常广泛。以下是一些常见的应用场景：

1. 经济学

指数函数在经济学中用于描述经济增长、人口增长、通货膨胀等现象。比如，一个国家的GDP增长率可以用指数函数来表示。

2. 生物学

指数函数在生物学中用于描述种群增长、病毒传播等现象。比如，一个细菌种群的增长可以用指数函数来描述。

3. 物理学

指数函数在物理学中用于描述放射性衰变、热力学过程等现象。比如，放射性物质的衰变可以用指数函数来描述。

指数函数，这个数学界的明星，以其独特的魅力和强大的能力，为我们的生活带来了无尽的惊喜。让我们一起探索它的奥秘，感受数学的无限魅力吧！